LeetCode 笔记

本文最后更新于：2022年7月31日 晚上

1. 两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案 202203021820930

链接：https://leetcode-cn.com/problems/two-sum

解法：

常规思路是使用两个for循环，遍历数组中的组合方式，返回满足结果的答案；

时间复杂度是\(O(n^2)\);

核心代码

1
2
3
4
5
6
7
8
9
10
11
for (int i = 0; i < numslength; i++)
{
    for (int j = i; j < numslength; j++)
    {
        if(nums[i]+nums[j]==target && i!=j)
        {
            res.emplace_back(i);
            res.emplace_back(j);
        }
    }
}

第二种解法，使用map数据结构，<key,value>=<nums[i],index>;遍历数组，使用count();计算target-nums[i]的个数，使用map在\(O(1)\)的时间复杂度内找到taget-nums[i]的index;

因为count()函数时间复杂度为\(O(\log ^{n})\),总的时间复杂度为\(O(n\log{n})\);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 vector<int> twoSum(vector<int>& nums, int target){
    vector<int> res;
    map<int, int> M;
    int numslength = nums.size();
    for (int i = 0; i < numslength;++i){
        M.insert({nums[i], i});
    }
    for(int i = 0; i < numslength;++i)
    {
        int numsOfOther = M.count(target - nums[i]);
        if(numsOfOther>0&&(M[target - nums[i]]!=i)){
            res.emplace_back(i);
            res.emplace_back(M[target - nums[i]]);
            break;
        }
    }
}

2.两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

202203021937657 链接：https://leetcode-cn.com/problems/add-two-numbers

解题

难点在于返回的是一个指针

建立一个头节点，使用while循环，遍历两个数组，对应数字相加，mod 10放入新链表，、10与下一组累加；同时在循环外判断最后一个数在/10是否大于0，如果大于0，新加一个节点；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
struct ListNode
{
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

ListNode *addTwoNumbers(ListNode *l1, ListNode *l2)
{

    ListNode *prehead = new ListNode(0);
    ListNode *cur = prehead;

    int t = 0;
    while (l1 || l2)
    {
        if (l1)
            t += l1->val, l1 = l1->next;
        if (l2)
            t += l2->val, l2 = l2->next;  // 一般情况下 t += (A[i] + B[i])后是一个0-19大的数字，个位push到当前位，而十位只有0和1作为进位继续后面的加法
        cur->next = new ListNode(t % 10); // t % 10 是 t的个位
        cur = cur->next;
        t /= 10; // t/=10，计算是否有进位，并更新t, 在下一轮继续 t += (A[i] + B[i])
    }
    if (t)
    {
        cur->next = new ListNode(t);
    } // 别忘了如果最后一位加法完成后，还得考虑进位
    return prehead->next;
}

3. 无重复字符的最长字串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

202203021951814
202203021952737

解题：

使用滑动数组解决

定义一个数组numOfCha用来记录每种字母与空格的数量，定义leftIndex标记子串的左界

使用for循环遍历字符串：如果遍历到的字符已出现次数为0,子串向右加一，numOfCha更新，计算长度(i-letIndex+1)，更新最大长度；否则不断弹出最左侧的字符，leftIndex++,相当于向右滑动；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int lengthOfLongestSubstring(string s)
{
    int leftIndex=0, maxLength=0;
    int len = s.size();
    int numOfCha[100];
    memset(numOfCha, 0, sizeof(numOfCha));
    set<char> m;
    for (int i = 0; i < len;i++)
    {
      while (numOfCha[s[i]-' ']!=0)
      {
          numOfCha[s[leftIndex] - ' ']--;
          leftIndex++;
      }
      maxLength = max(maxLength, i - leftIndex + 1);
      numOfCha[s[i] - ' ']++;
    }
    return maxLength;
}

5. 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串

image-20220302214119440

解法：

  • 扩展中心

    我们知道字符串一定是对称的，所以我们可以每次循环的时候选择一个中心，进行左右扩展，判断新扩展的字符是否相等。

    202203041856092

    因为存在奇数的字符串或者偶数的字符串，所以我们需要从一个字符开始扩展，或者两个连续的字符开始扩展，所以共有n + (n-1)个中心。

    时间复杂度：O(\(n^2\)）O(\(n^2\)）。

    空间复杂度：O(1）O(1）。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    int expendAroundCenter(string s, int lef, int rig)
    {
        int subLef = lef;
        int subRig = rig;
        // 左界应该在大于等于0，右界应当小于字符串的长度，同时新扩展的两个字符应当相等
        while ((subLef >= 0) && (subRig < s.length()) && (s[subLef] == s[subRig]))
        {
            subLef--;
            subRig++;
        }
        //返回的是以s[lef,rig]为中心的回文子串长度
        return subRig - subLef + 1;
    }

    //主函数
    string longestPalindrome(string s)
    {	
        //如果S是空，则返回空
        if (s == "" || s.length() < 1)
            return "";
        //用来标记最长回文子串的左右界
        int strStart = 0, strEnd = 0;
        
        int strLen = s.length();
    	//遍历每一个字符
        for (int i = 0; i < strLen; i++)
        {	
            //以该字符为中心，或者连续两个字符为中心
            int len1 = expendAroundCenter(s, i, i);
            int len2 = expendAroundCenter(s, i, i + 1);
            int len = max(len1, len2);
            //如果长度大于我们标记的，更新左右界
            if (len > strEnd - strStart + 1)
            {
                strStart = i - (len - 1) / 2;
                strEnd = i + len / 2;
            }
        }
        return s.substr(strStart, strEnd - strStart + 1);
    }

8. 字符串转整数

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。

函数 myAtoi(string s) 的算法如下：

  1. 读入字符串并丢弃无用的前导空格
  2. 读入下一个字符，确定正负号，若不存在假定为正
  3. 读入数字转化为整数，无数字则为0
  4. 若溢出int,则截断整数

输入: s=“ -42 akkk”

输出: -42

输入: s="-2147483648"

输出: -2147483648

输入: s=“ 2147483648”

输出: 2147483648

链接：https://leetcode-cn.com/problems/string-to-integer-atoi

解法：

思路较为清晰和明确，整体是遍历一遍字符串

首先去除开头的空格，index++;

如果index==len,全是空格，则返回0；

之后判断正负，使用sign标定

转化数字时因为只能使用32位，所以判断时应该与INT_MAX/10比较，因为INT数字范围是\(\left[ -2^{32},2^{32}-1 \right]\)，所以在判断个位数时应该使用大于

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
int myAtoi(string s)
{
    int len = s.length();
    int index = 0, sign = 1, res = 0;
    //如果是空格，索引向后
    while (s[index] == ' ' && index < len)
    {
        index++;
    }
    if (index == len)
    { //整个字符串都是空格
        return 0;
    }
    else
    {
        if (s[index] == '-')
        { //是否为负数
            sign = -1;
            index++;
        }
        else if (s[index] == '+')
        { //是否为正数
            index++;
        }
        while (index < len && s[index] <= '9' && s[index] >= '0')
        {
            int curDigit = s[index] - '0';
            if (res > INT_MAX / 10 || ((res == INT_MAX / 10) && (curDigit > INT_MAX % 10)))
            {
                return sign==1?INT_MAX:INT_MIN;
            }
            else
            {
                res = res * 10 + curDigit;
            }
            index++;
        }
        return sign * res;
    }
}

14. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""

image-20220315151908284

题目链接：https://leetcode-cn.com/problems/longest-common-prefix/

解法：

1. 暴力

首先，我们可以找到最短串的长度minStrLen，这样在比较每个字母是就不用担心会溢出

然后，遍历每个字符串，当同一index的字母相同时，res加上该字母，否则break

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
string longestCommonPrefix(vector<string>& strs) {
       string res = "";
       int minStrLen = 300;
       for (int i = 0; i < strs.size(); i++)
       {
           int indexLen = strs[i].size();
           if (indexLen < minStrLen)
           {
               minStrLen = indexLen;
           }
       }

       for (int i = 0; i < minStrLen; i++)
       {
           bool flag = true;
           for (int j = 0; j < strs.size() - 1; j++)
           {
               if(strs[j][i]!=strs[j+1][i])
               {
                   flag = false;
                   break;
               }
           }
           if(flag)
               res += strs[0][i];
           else
               break;
       }
       return res;
}

这样的结果为

image-20220315161954911
2. 字典序排序

在对字符串进行sort时，是按照字典序，所以我们完全可以在排序后比较第一个和最后一个的公共前缀子串，这样就可以省去比较每一个字符串的问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
string longestCommonPrefix(vector<string> &strs)
{
    sort(strs.begin(), strs.end());
    string res;
    string first = strs.front();
    string end = strs.back();
    for (int i = 0; i < first.size() && i < end.size();i++)
    {
        if(first[i]!=end[i]){
            break;
        }
        res += first[i];
    }
    return res;
}
image-20220315162405643

这样极大的缩短了代码量，大佬们的脑洞太大了

15. 三数之和

题目描述

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例

1
2
3
4
5
6
7
给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]

题目解析

最容易想到的就是三重循环暴力法搜索，时间复杂度为 O(n^3). 有点高啊，优化一下.

通过题目我们了解到，主要问题在于 搜索所有满足条件的情况 和 避免重复项，那么我们可以使用 升序数组 + 双指针 有效处理问题并降低时间复杂度.

你可能想知道为啥会选择使用这个方案 ？

首先数组排序时间复杂度可以达到 O(NlogN)，这点时间消耗我们是能接受的，另外根据有序数组的特性，数组重复项会挨在一起，不需要额外的空间存储就能跳过重复项，由于是升序，当发现最左边的数值大于0，就可以及时跳出来结束运算.

双指针可以用来降维. 通过遍历数组，取当前下标值为定值，双指针代表定值后面子数组的首尾数值，通过不断靠近双指针来判断三个值的和。

具体算法流程如下：

  1. 特判：对于数组长度 n，如果数组为 null 或者数组长度小于 3，返回[ ] ;
  2. 数组升序排序；
  3. 遍历数组：
    • 若 num[i] > 0：因为是升序，所以结果不可能等于0，直接返回结果；
    • 令左指针 L = i + 1，右指针 R = n - 1，当 L < R 时，执行循环：
      • 当 nums[i] + nums[L] + nums[R] == 0 ，执行循环，判断左指针和右指针是否和下一位置重复，去除重复解。并同时将 L,R 移到下一位置，寻找新的解；
      • 若和大于 0，说明 nums[R] 太大，R指针 左移
      • 若和小于 0，说明 nums[L] 太小，L指针 右移

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
vector<vector<int>> threeSum(vector<int> &nums)
{
    vector<vector<int>> res;
    sort(nums.begin(), nums.end());
    if (nums.size() == 0 || nums.back() < 0 || nums.front() > 0)
        return res;
    for (int k = 0; k < nums.size(); k++)
    {
        if (nums[k] > 0)
            break;
        //去重操作，如果是nums[k]==nums[k+1],会忽略-1，-1，2这样的情况
        if (k > 0 && nums[k] == nums[k - 1])
            continue;
        int target = 0 - nums[k];
        int i = k + 1, j = nums.size() - 1;
        while (i < j)
        {
            if (nums[i] + nums[j] == target)
            {
                res.push_back({nums[k], nums[i], nums[j]});
                //因为返回的是数组中的数，所以相同的数我们只需要一个
                while (i < j && nums[i] == nums[i + 1])
                    ++i;
                while (i < j && nums[j] == nums[j - 1])
                    --j;
                ++i;
                --j;
            }
            else if (nums[i] + nums[j] < target)
                ++i;
            else
                --j;
        }
    }
    return res;
}

19 删除链表的倒数第 N 个节点

题目描述

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

1
2
3
给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：

给定的 n 保证是有效的。

进阶：

你能尝试使用一趟扫描实现吗？

题目解析

采取双重遍历肯定是可以解决问题的，但题目要求我们一次遍历解决问题

解法一 两次遍历

这也是最naive的解法，第一次遍历找到链表的长度，第二次遍历到需要删除节点的前一个节点，使用next指针将所需要删掉的节点绕过。

需要考虑只存在一个节点或者删除的就是头节点的特殊情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode *cur = head;
        int nums = 1;
        while (cur->next != nullptr)
        {
            cur = cur->next;
            nums++;
        }
        if(nums==1||nums-n==0)
            return head->next;
        // 到删除节点的前一个
        int index = 1;
        cur = head;
        while (index < (nums - n))
        {
            cur = cur->next;
            index++;
        }

        ListNode *ptr = cur->next;
        cur->next = ptr->next;
        return head;
}

解法二 快慢指针

很容易就可以想到我们何不声明一个快慢指针，快指针比慢指针领先n个进度，当快指针指向最后一个时，慢指针指向我们需要删掉的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
ListNode* removeNthFromEnd(ListNode* head, int n) {
    	//无节点或者只有一个头节点
        if(!head | !head -> next) return NULL;
        ListNode * fast = head, *slow = head;
        for(int i = 0; i < n; i++){
            fast = fast -> next;
        }
        //链表长度小于n时，相当于删掉头节点
        if(!fast){
            return head -> next;    
        }
        //找到我们需要的节点
        while(fast -> next){
            fast = fast -> next;
            slow = slow -> next;
        }
        slow -> next = slow -> next -> next;
        return head;
    }

解法三 递归

因为递归过程，所以我们实际上首先找到的是链表的最后一个，并向前回溯，回溯过程中cur++；当找到我们应该删掉的节点时，返回的实际上是next指针，相当于返回了下一个节点，等价于删除操作；正常应该返回的是当前节点。

1
2
3
4
5
6
7
8
9
10
11
int cur = 0;
ListNode *removeNthFromEnd(ListNode *head, int n)
{
    if (!head)
        return NULL;
    head->next = removeNthFromEnd(head->next, n);
    cur++;
    if (n == cur)
        return head->next;
    return head;
}

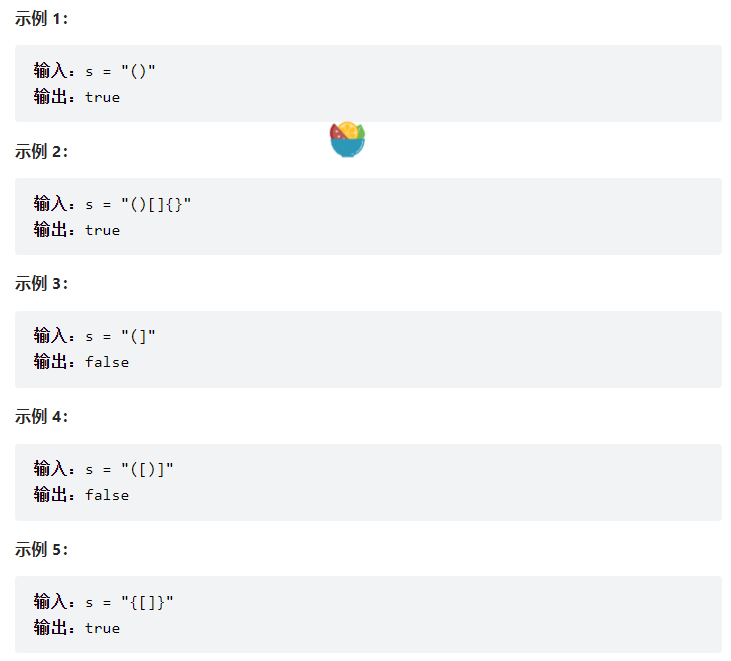
20. 有效的括号

题目描述

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

  • 左括号必须用相同类型的右括号闭合。
  • 左括号必须以正确的顺序闭合。

样例

image-20220326142418796

链接：https://leetcode-cn.com/problems/valid-parentheses

思路

这是一道栈的经典题型

这道题让我们验证输入的字符串是否为括号字符串，包括大括号，中括号和小括号。我们使用栈来存储括号

  • 遍历输入字符串
  • 如果当前字符为左半边括号时，则将其压入栈中
  • 如果遇到右半边括号时，分类讨论：
  • 1）如栈不为空且为对应的左半边括号，则取出栈顶元素，继续循环
  • 2）若此时栈为空，则直接返回false
  • 3）若不为对应的左半边括号，反之返回false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
bool isValid(string s)
{
    int len = s.size();
    if (len % 2 != 0)
        return false;
    stack<char> brackets;
    for (int i = 0; i < len; i++)
    {
        //遇到左括号压入栈
        if (s[i] == '{' || s[i] == '(' || s[i] == '[')
            brackets.push(s[i]);
        //右括号分情况
        else
        {
            //情况1:栈为空，没有与右括号匹配，返回false
            if (!brackets.size())
                return false;
            char cur = brackets.top(), match;
            brackets.pop();
            //匹配的左括号
            if (s[i] == ')')
                match = '(';
            else if (s[i] == ']')
                match = '[';
            else
                match = '{';
            //情况2:扫描到的右括号所匹配的左括号！= 栈顶括号
            if(match !=cur)
                return false;
        } 
    }
    // 扫描完字符串，是否清空栈
    return brackets.size() == 0;
}

// 第二种代码写法
bool isValid(string s)
{
    int len = s.size();
    if (len % 2 != 0)
        return false;
    stack<char> brackets;
    for (int i = 0; i < len; i++)
    {
        // 将左括号匹配的右括号压入栈
        if (s[i] == '(')
            brackets.push(')');
        else if (s[i] == '{')
            brackets.push('}');
        else if (s[i] == '[')
            brackets.push(']');
        // 扫描遇到右括号
        else
        {
            if (!brackets.size())
                return false;
            else if (brackets.top() != s[i])
                return false;
            else
                brackets.pop();
        }
    }
     return brackets.size() == 0;   
}

21 合并两个有序链表

题目描述

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

image-20220326143806602

一般思路

  1. 比较链表1和链表2的第一个结点的值，将值小的结点保存下来为合并后的第一个结点。并且把第一个结点为最小的链表向后移动一个元素。
  2. 继续在剩下的元素中选择小的值，连接到第一个结点后面，并不断next将值小的结点连接到第一个结点后面，直到某一个链表为空。
  3. 当两个链表长度不一致时，也就是比较完成后其中一个链表为空，此时需要把另外一个链表剩下的元素都连接到第一个结点的后面。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
ListNode *mergeTwoLists(ListNode *list1, ListNode *list2)
{
    ListNode *newList = new ListNode(0);
    ListNode *dummyhead = newList, *p = list1, *q = list2;
    while (p && q)
    {
        if (p->val <= q->val)
        {
            newList->next = new ListNode(p->val);
            p = p->next;
        }
        else
        {
            newList->next = new ListNode(q->val);
            q = q->next;
        }
        newList = newList->next;
    }
    if(p)
        newList->next = p;
    else
        newList->next = q;
    return dummyhead->next;
}

递归实现

（1）对空链表存在的情况进行处理，假如 list1 为空则返回 list2 ，list2 为空则返回 list1。 （2）比较两个链表第一个结点的大小，确定头结点的位置 （3）头结点确定后，继续在剩下的结点中选出下一个结点去链接到第二步选出的结点后面，然后在继续重复（2 ）（3） 步，直到有链表为空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ListNode *mergeTwoLists(ListNode *list1, ListNode *list2)
{
    if (list1 == nullptr)
        return list2;
    if (list2 == nullptr)
        return list1;
    if (list1->val < list2->val)
    {
        list1->next = mergeTwoLists(list1->next, list2);
        return list1;
    }
    else
    {
        list2->next = mergeTwoLists(list1, list2->next);
        return list2;
    }
}

25 生成括号

题目描述

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

image-20220407162502848

动态规划

核心思路：考虑 i=n 时相比 n-1 组括号增加的那一组括号的位置

i<n 的情况，那我们就可以对所有情况进行遍历：

"(" + [i=p时所有括号的排列组合] + ")" + [i=q时所有括号的排列组合]，其中 p + q = n-1，且 p q 均为非负整数。

事实上，当上述 p 从 0 取到 n-1，q 从 n-1 取到 0 后，所有情况就遍历完了。

注：上述遍历是没有重复情况出现的，即当 (p1,q1)≠(p2,q2) 时，按上述方式取的括号组合一定不同。

因为我们实际上是得出了从2-n的所有答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<string> generateParenthesis(int n) {
    if (n == 0)
        return {};
    if (n == 1)
        return {"()"};
    vector<vector<string>> dp(n + 1);
    dp[0] = {""};
    dp[1] = {"()"};
    for (int i = 2; i <= n; i++) { //从2-n一步步向上迭代
        for (int j = 0; j <= i - 1; j++) {
            for (const auto &value1 : dp[j]) {
                for (const auto &value2 : dp[i - 1 - j]) {
                    dp[i].emplace_back('(' + value1 + ')' += value2);
                }
            }
        }
    }
    return dp[n];
}

递归

使用dfs进行，每次递归的时候，先一直加上(，再一直加上)

需要注意的是，在进行递归的时候，对于string类型的参数，当传参的时候，不能传入引用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void dfs(vector<string> &res, string s, int l, int r, int n) {
    if (l > n || r > n)
        return;
    if ((l == r) && (l == n)) {
        res.emplace_back(s);
        return;
    }
    dfs(res, s + "(", l + 1, r, n);
    dfs(res, s + ")", l, r + 1, n);
}

vector<string> generateParenthesis(int n) {
    vector<string> res;
    dfs(res, "", 0, 0, n);
    return res;
}